考虑定向能量沉积工艺特点的减材加工余量优化
时间：2022-10-13 11:08 来源：未知 作者：admin 阅读：次
激光定向能量沉积(directed energy deposition，DED)利用激光熔融金属粉末，逐层堆叠三维实体。相比激光选区融化增材制造技术(selective laser melting，SLM)，DED单道增材宽度及单层抬升高度可达毫米级，具有更高的成形效率。结合多轴联动，DED可实现无支撑制造复杂悬垂零件，成形自由度高，但高沉积效率也造成零件表面粗糙，存在明显台阶效应。当沉积零件为复杂悬垂类零件时，台阶效应更加明显[1]。另外，受快速凝固、热棘轮效应等成形机理影响，零件易产生严重热变形[2-3]。为此，DED增材制造零件一般都需要减材加工工艺以保证制造精度[4]。
因变形、台阶效应及其他制造缺陷，复杂悬垂类零件余量常偏离理论加工余量，可能造成单边减材加工余量不足，进而导致整个零件报废。为避免上述情况，常扩大设计模型以增大减材后处理余量，但同时也使加工效率降低，刀具损耗增大。解决该问题需准确获取DED制造毛坯轮廓，并利用余量优化技术提高加工效率、降低刀具及工件损耗。毛坯成形精度获取方法包括仿真预测及精密测量技术。仿真预测常通过构建精确的热力仿真模型来预测变形[5]，但现有增材仿真技术仍然很难高效处理多轴联动制造的复杂大型零件问题[6]。另一方面，集成于增减材复合装备上的在机测量技术，可有效评估复杂零件成形精度，避免离线检测带来的重复定位误差。同时，基于在机检测获取的毛坯轮廓点位信息，通过点云配准技术，可优化因成形机理、制造缺陷、增材工艺规划等原因造成的局部余量不足或过大等问题[7]。
逐层堆叠的成形原理造成复杂曲面类零件台阶效应明显。在DED近净成形中，台阶效应对后处理余量影响不能忽视。为此，AHN等[8]提出了考虑熔融沉积成形工艺(fused deposition modeling，FDM)中丝材截面形状、重叠率及层厚等工艺参数对表面形貌作用的模型，可预测台阶效应引起的表面粗糙度。KAJI等[9]利用表面斜率与单层厚度构建了表面形貌经验模型，结果表明，单层厚度越大，台阶效应越明显。因而降低单层厚度，可提高表面质量，但也牺牲了成形效率。需要指出，以上形貌经验模型仍较难推广到复杂自由曲面形貌表征。另一方面，台阶效应等引起的粗糙表面形貌与扫描路径直接关联，利用扫描路径构建在机测量路径，可准确定位至台阶效应波谷处。因台阶效应波谷处为余量控制的关键处，决定了DED毛坯的最小轮廓，因此，基于台阶效应波谷处的测量路径可精确获取毛坯最小轮廓点云，避免余量优化过程中因测量失真导致的余量不足、余量不均等问题。
基于点云配准的加工余量优化通过设置合理余量优化目标，寻求毛坯与理论模型的最优变换矩阵。三维点云配准技术在余量优化研究中应用广泛。SHEN等[10]提出一种最优位置拟合算法以改善负余量问题，但不适用于增材制造粗糙表面。LI等[11]利用复杂模型中平面特征对精密铸件进行配准，计算效率高，但未均匀化加工余量，且只适用于有平面特征的工件。SUN等[12]将乘子法与拟牛顿法算法相结合，简化定位中的复杂约束问题，但该方法更适用于单侧余量优化。张莹等[13]、YING等[14]给出了加工余量优化的统一数学模型，将典型定位余量优化问题分类，分别构造约束函数，并提出分块对称法求解优化模型。张明德等[15]利用曲面匹配技术获取各刀触点实际余量，优化刀路实现自适应减材加工，实现余量优化。GAO等[16]以精密铸件为研究对象，提出基于遗传算法的多目标余量优化方法，是一种求解余量优化问题的通用算法。综上，目前对DED制造复杂自由曲面零件的工艺特点及相应余量优化技术鲜有研究。
本文提出一种考虑增材制造特点的在机检测方法，该方法先沿台阶效应波谷处构建测量路径，确定DED毛坯件最小轮廓。然后，根据不同区域余量要求，将点云划分为待加工区域与定位区域，引入中面动态配准法平衡不同区域加工余量优化中的博弈问题。最后，通过实例分析验证所提测量方法的有效性。
1 理论方法
1.1 考虑增材特征的在机检测
DED制造复杂悬垂曲面类零件时台阶效应明显。为提高沉积效率，送粉率、抬升高度等取值需相应增大，造成该类零件台阶效应更为明显，表面波峰和波谷交替变化，如图1所示，可以看出，波谷决定了沉积件的最小轮廓。若测量路径不平行于台阶效应走向，会使局部区域检测到最大轮廓处，进而导致余量优化中局部区域加工余量不足、余量不均匀等问题。为此，提出考虑台阶效应的在机检测规划方法(图2)，即沿台阶效应波谷处构建最小轮廓规划检测路径。
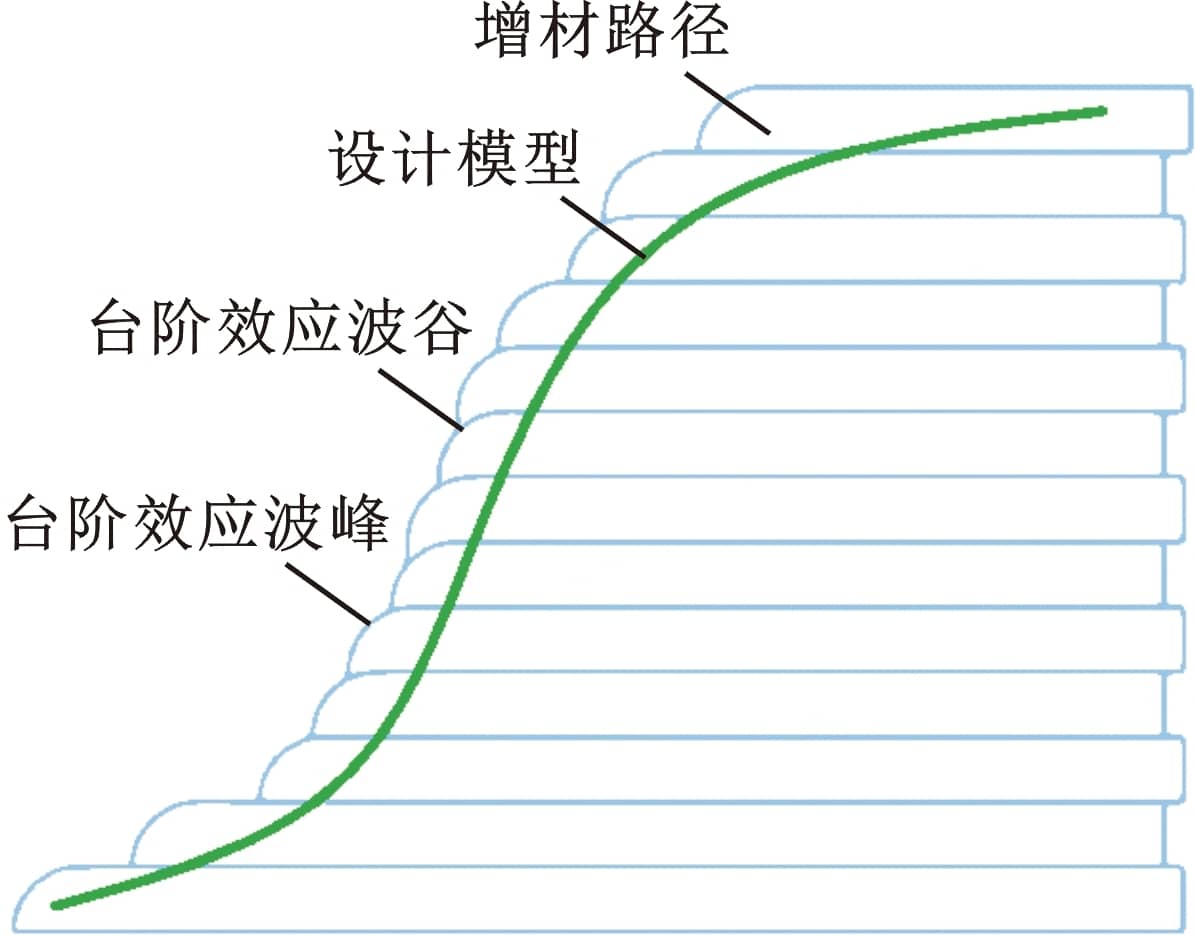
图1 台阶效应原理
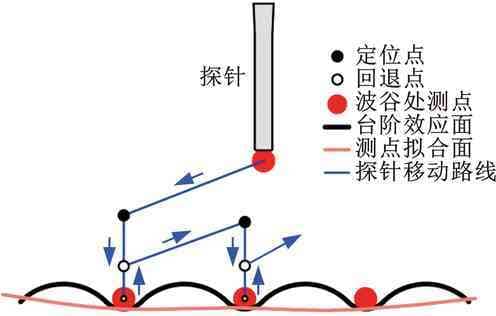
图2 在机检测策略
测量截面线与测点是影响测量精度的关键因素。传统截面线构造方法包含等高法、等半径法、等参数法等[17]，但均难以保证定位到DED毛坯最小轮廓。本文提出考虑增材制造特点的DED复杂曲面零件在机检测方法，测量流程如图3所示。第一步，在PowerMill中规划增材制造路径，运动仿真以生成无碰撞增材制造路径，成形的复杂曲面沉积零件存在明显台阶效应。第二步，提取最外层增材路径作为初始截面线，依据DED抬升高度偏置初始截面线，以定位至台阶效应波谷处，获得基于最小轮廓的测量截面线；为防止复杂曲面零件测量失真，采用弦高度差法自适应规划截面线上测点[17]；在PowerInspect环境中规划测点对应的检测组，设置测量参数，后处理生成无碰撞在机检测代码，完成测量。
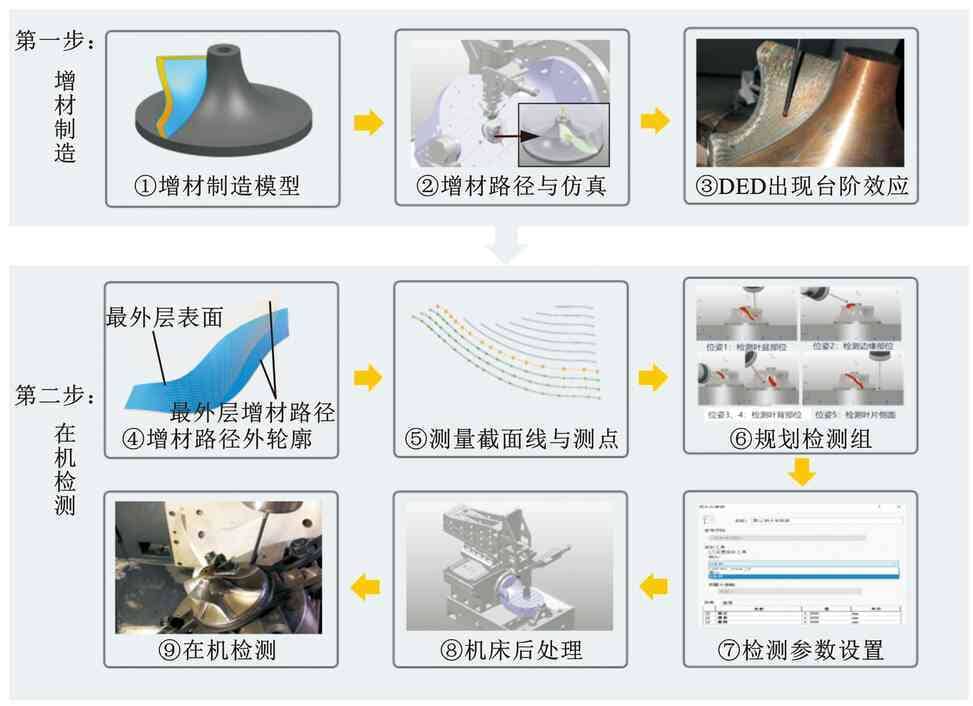
图3 考虑台阶效应的在机检测规划流程
1.2 基于中面动态配准的余量优化方法
DED成形零件余量优化需同时考虑余量均匀性、基准定位原则及包络原则。设测量点云P={pn}，n=1，2，…，N，理论模型点云Q={qn}，pn和qn为对应点云集合内一点，如图4所示。余量均匀性要求点云P到Q的变换矩阵R、T使匹配点对(pn，qn)距离的方差最小：
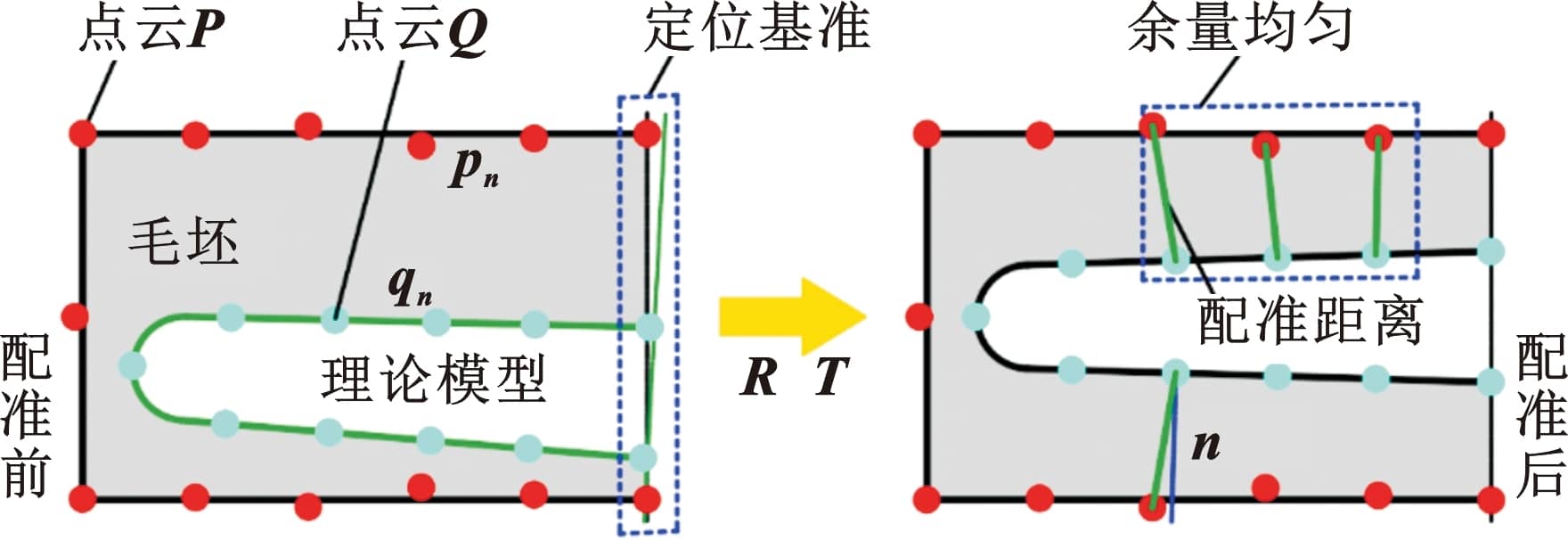
图4 点云配准示意图
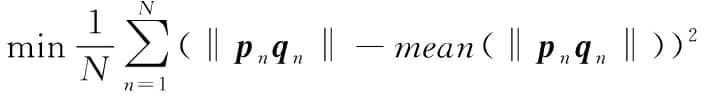(1)
增减材复合制造中，增材沉积和减材加工共享同一定位基准，因而，不同于其他待减材加工区域，定位基准的配准精度要求严苛。设定位基准有N′ 对配准点，余量优化过程中应使N′ 组配对点的距离和足够小：
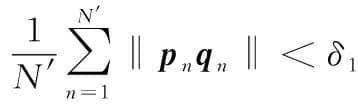(2)
包络原则要求待减材区域测点均位于理论模型轮廓外，保证留有加工余量：
pnqn·n>δ2(3)
式中，n为理论模型在点qn处的单位外法矢；δ2必须大于0。
对于双侧需减材加工的叶片类零件，以测点拟合中面和理论模型中面进行余量优化，从而减少余量优化过程中配准点数量，提高计算效率。图5中面点云width=176,height=17,dpi=110分别从测量点云P及理论模型中提取，该过程在MATLAB 2019环境中实现。设中面配准中共有M组配准点，其中定位区域I对，其余待加工区域J对。为满足余量均匀性和外包络原则，各中面配对点间距离不能超过特定阈值δ3：
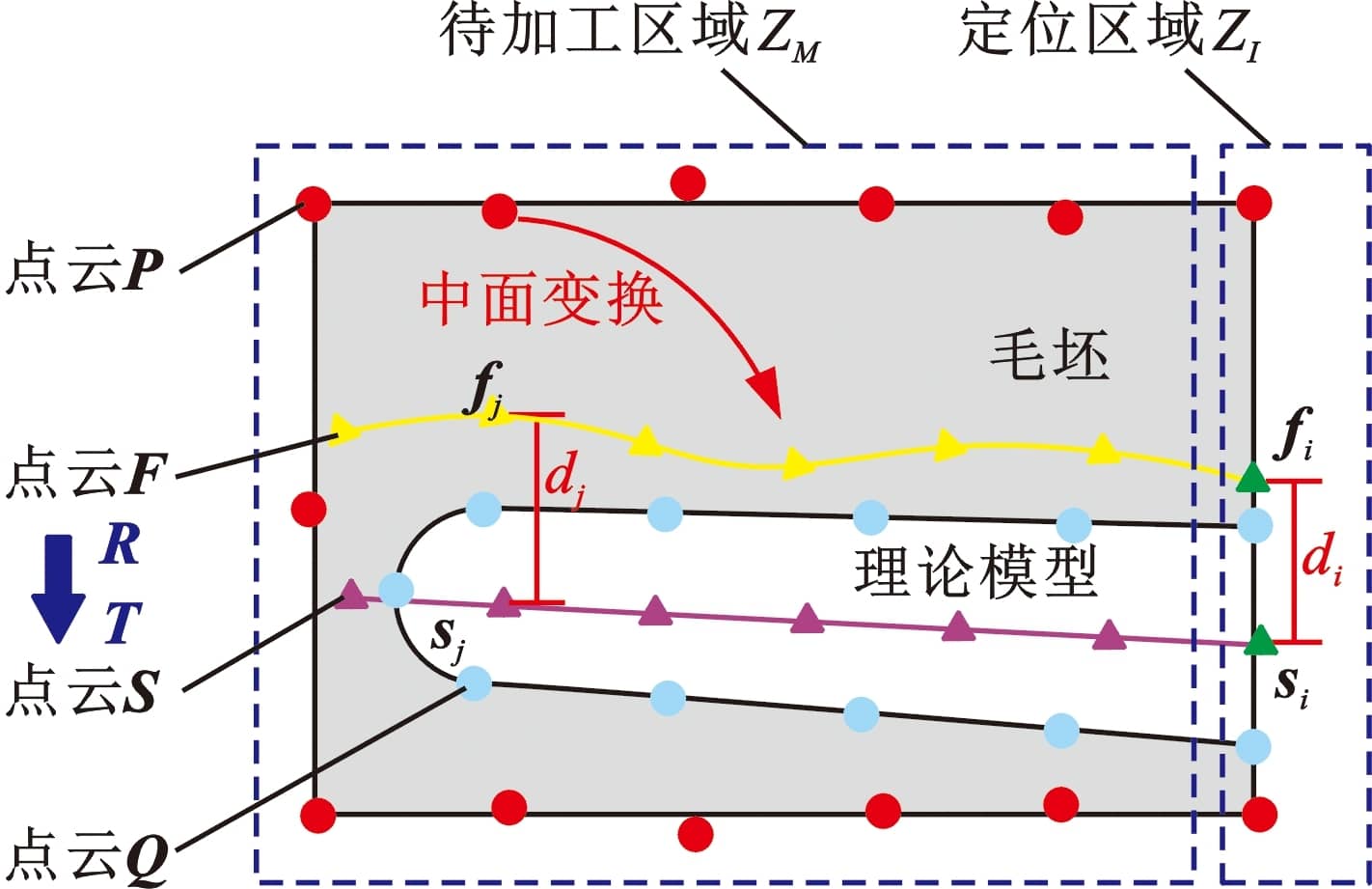
图5 中面配准原理
‖smfm‖<δ3(4)其中，δ 3依据定向能量沉积零件的理论制造余量确定。中面配准情况下，定位约束条件式(2)表示为width=146,height=40,dpi=110可以看出，以中面点云替代全局点云，不仅减少了待配准点云数量，且将约束条件式(1)、式(3)统一成式(4)，具有计算效率高、实现简便等优点。
中面配准使测点到理论模型的余量优化问题简化为不同区域配准精度的博弈问题。定位区域需满足式(2)定义的精度要求，待加工区域满足式(4)。为此，引入动态权重因子自适应平衡不同配准精度在点云匹配迭代中的博弈[18-19]。适用不同配准精度要求的中面余量优化目标为
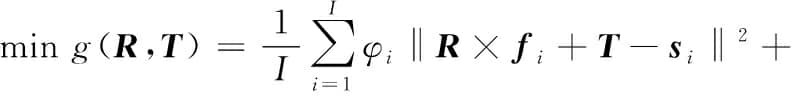
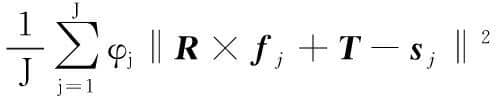
(5)
式中， φi为定位区域内i点权重因子； φj为加工区域内j点权重因子。当目标区域内点超出式(2)和式(4)规定的阈值δ1或δ3时，权重因子相应增大，从而改变该点在目标函数中占比。权重因子动态调整准则为
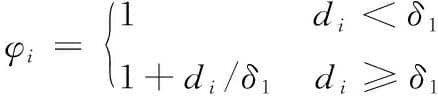
(6)
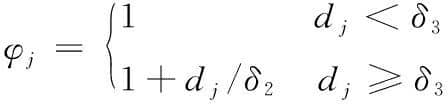
(7)
式中，di、dj分别为定位及加工区域内配准点距离。由式(2)、式(4)及式(5)～式(7)定义的中面动态配准问题可采用迭代最近邻点(iterative closest point，ICP)算法[20]求解，配准具体过程如下。
(1)求最近邻点及更新权重因子。设ICP算法第k-1次迭代的旋转和平移矩阵分别为Rk-1和Tk-1。利用KD-Tree(K-dimensional tree)算法[21]搜索第k-1次迭代中面测点Fk-1{Rk-1fm+width=61,height=17,dpi=110上每一点在S中最近邻点，并计算不同区域最近邻点对距离di,k-1和dj,k-1。依据式(6)和式(7)更新不同区域各点权重因子φi，k-1、φj，k-1。
(2)计算第k次迭代的变换矩阵Rk、Tk。利用步骤(1)中各权重因子φi，k-1、φj，k-1及Fk-1更新式(5)，并通过SVD(singular value decomposition)法[22]求解，获取Rk、Tk，并根据所求矩阵更新点云Fk。
(3)计算第k次变换配准点对距离di，k、dj，k。判断是否满足距离约束di，k<δ1、dj,k<δ3。若满足，则计算配对点距离的平均误差width=255,height=41,dpi=110当|ek+1-ek|小于阈值ε时停止迭代，否则重复步骤(1)～(3)。
(责任编辑：admin)
适配多类别高温聚合物FFF
埃肯与Startuplab合作加速
NAMIC 全球增材制造峰会GA
3iD率先引进全新粘结剂喷
Freeform人工智能3D打印工
Biomaterials science:牛最新内容
卡内基梅隆研究人
Align Technology
AM Craft在种子轮
Aerojet拿下五角
印度初创公司在Gi
美军使用金属3D打热点内容
